摘要:最小二乘法、岭回归、Lasso的区别在于损失函数不同,本文+代码实例演示岭回归和Lasso,最后小结。
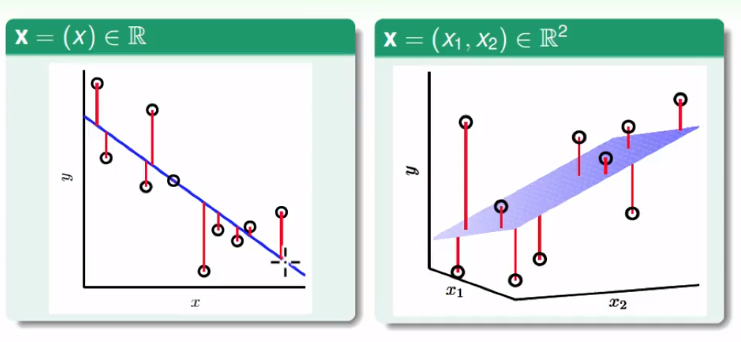
欧式距离图
上篇回顾:[代码实例]机器学习线性回归之最小二乘法
一、数据集来源及格式
与上篇相同,根据前4个特征预测发电量
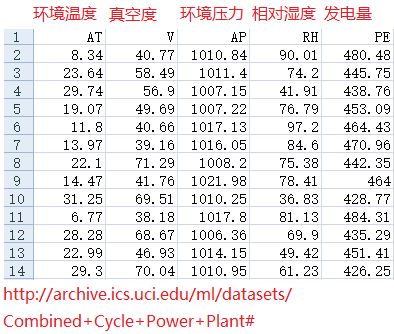
数据集格式及来源
使用画出各特征与PE关系图:

可得各特征与PE关系图:
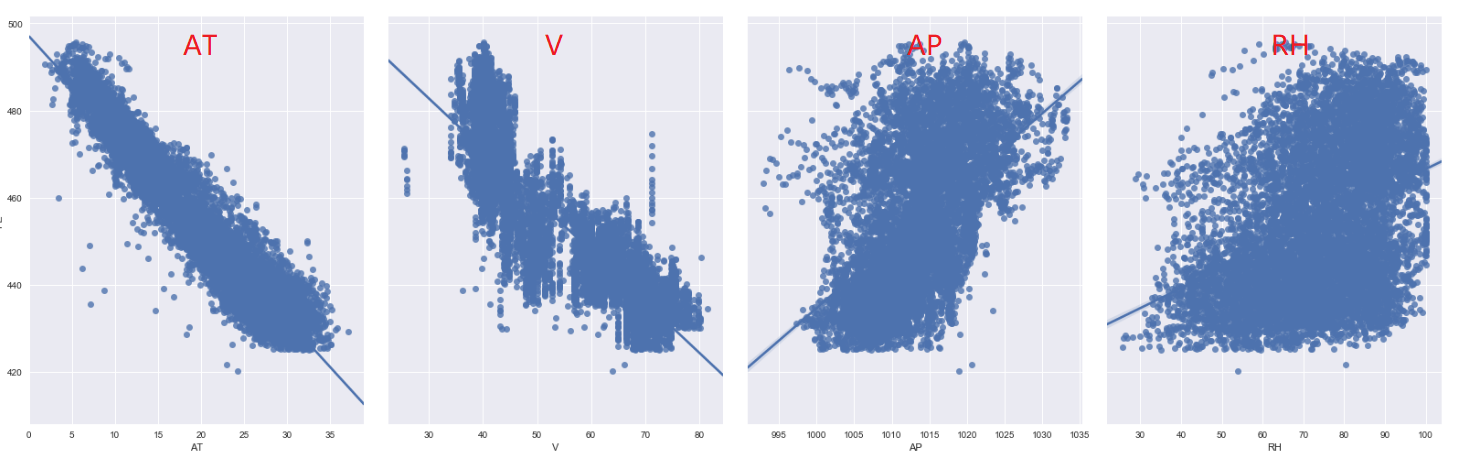
各特征与PE关系图
请留意上图于权重的关系。
二、岭回归与lasso
岭回归的损失函数为平方损失 + 所有权重平方和 * λ , λ>0。
lasso的损失函数为平方损失 + 所有权重绝对值 * λ , λ>0。
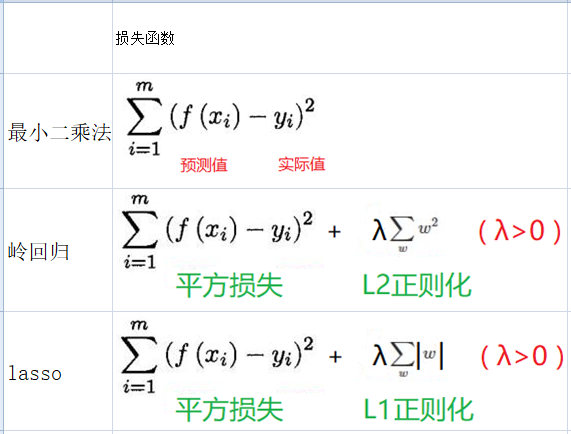
损失函数对比图
阅读过【一看就懂】机器学习之L1和L2正则化的朋友可知:
岭回归相当于在更新权重时每次移除权重的 x%;
lasso相当于在更新权重时每次递减(加)一个常数,使网络中的权重尽可能为0,因此可用于特征选择;
两者都是为了降低模型复杂度,提高泛化能力。
三、+代码:
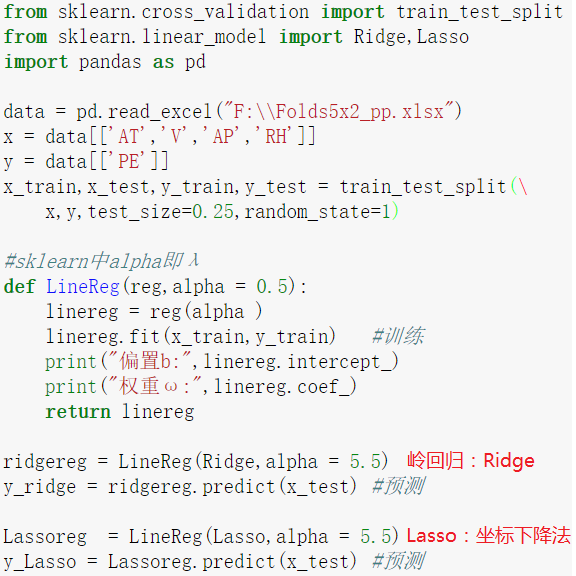
输出偏置和权重如下:

λ=5.5,岭回归与lasso权重
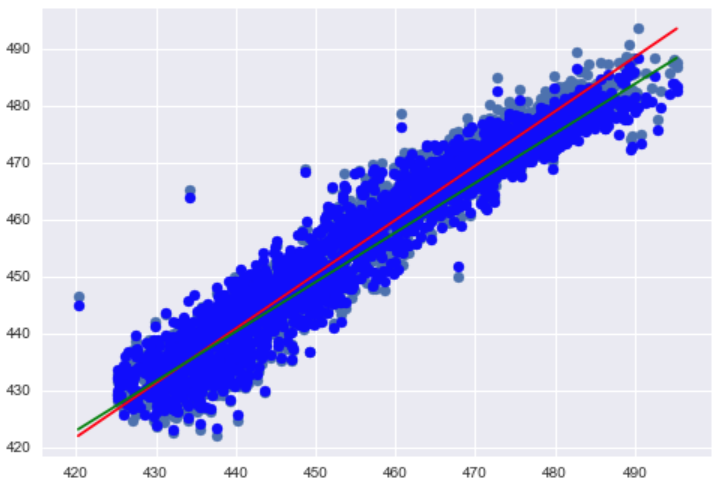
使用画出真实值和预测值的变化关系:

画图代码
图如下
四、三者什么时候更适用?
最小二乘法:特征独立分布,且与结果相关;
岭回归:特征之间具有强相关性;
Lasso:存在无关特征。
———END———
限 时 特 惠: 本站每日持续更新海量各大内部创业教程,永久会员只需109元,全站资源免费下载 点击查看详情
站 长 微 信: nanadh666
声明:1、本内容转载于网络,版权归原作者所有!2、本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。3、本内容若侵犯到你的版权利益,请联系我们,会尽快给予删除处理!



