施瓦兹空间、狄利克雷和若尔当定理是数学领域中的三个重要概念,它们在代数、几何和拓扑等领域有着广泛的应用。本文将依次介绍这三个概念,并探讨它们之间的联系与区别。
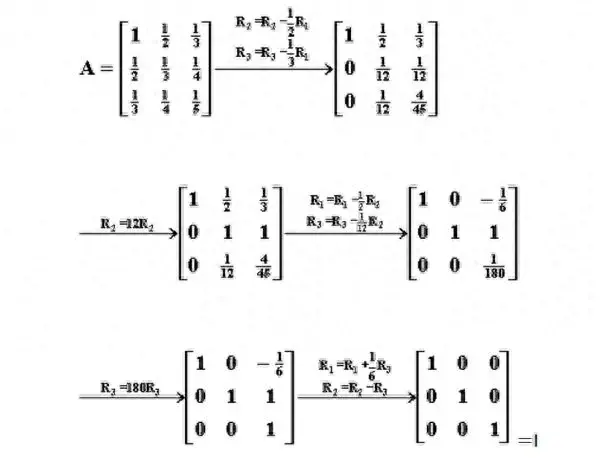
一、施瓦兹空间
施瓦兹空间是一种特殊的线性空间,它具有一些特殊的性质和结构。在施瓦兹空间中,向量之间的加法和数量乘法满足线性运算的规则,并且具有一些特殊的性质,如范数的存在性和三角不等式的性质。
施瓦兹空间在数学和物理领域有着广泛的应用。例如,在量子力学中,施瓦兹空间被用来描述量子态的数学结构;在微分几何中,施瓦兹空间被用来描述流形的切空间和余切空间。
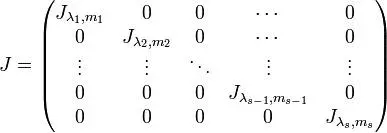
二、狄利克雷定理
狄利克雷定理是代数数论中的一个重要定理,它给出了一个域上的多项式方程的解的个数与该域的特征之间的关系。具体来说,如果一个域的特征为p,那么对于该域上的多项式方程,它的解的个数是p的倍数。
狄利克雷定理在代数数论中有着广泛的应用。例如,它可以用来判断一个多项式方程是否有解,也可以用来研究域的性质和结构。此外,它还可以用来解决一些著名的数学问题,如费马大定理。
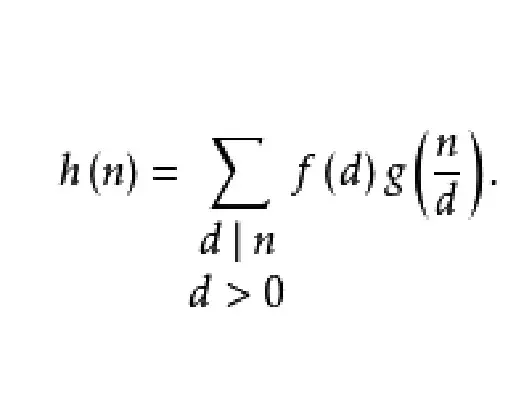
三、若尔当定理
若尔当定理是复分析中的一个重要定理,它给出了一个复平面上的闭曲线可以由其内部的点和该曲线上的一部分组成的区域进行表示。具体来说,如果一个复平面上的闭曲线C包围了一个区域D,那么D可以表示为C内部的所有点和C上的一段连续曲线所组成的区域。
若尔当定理在复分析中有着广泛的应用。例如,它可以用来研究复平面上的闭曲线的性质和结构;也可以用来解决一些著名的数学问题,如柯西积分公式和留数定理等。此外,若尔当定理还可以被推广到更一般的复流形上。
四、三者之间的联系与区别

施瓦兹空间、狄利克雷定理和若尔当定理虽然都是数学领域中的重要概念,但它们之间有着明显的区别。
施瓦兹空间是一种特殊的线性空间,它主要涉及到向量之间的加法和数量乘法;而狄利克雷定理是代数数论中的一个重要定理,主要涉及到域的特征和多项式方程的解的个数之间的关系;若尔当定理则是复分析中的一个重要定理,主要涉及到复平面上的闭曲线和区域的表示之间的关系。
然而,它们之间也存在着联系。例如,在复分析中,施瓦兹空间可以被用来描述复平面上的点集和曲线;而狄利克雷定理则可以被应用到复分析中,用来研究复平面上的闭曲线和区域的表示之间的关系。此外,这三个概念都需要使用代数运算和推理的方法来理解和应用。
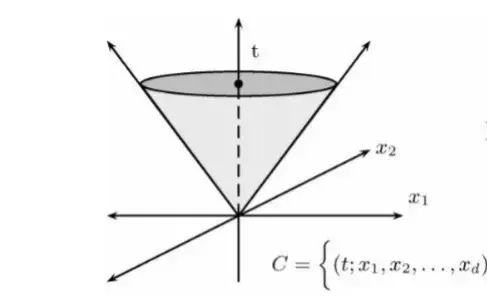
总之,施瓦兹空间、狄利克雷定理和若尔当定理是数学领域中的三个重要概念,它们各自有着独特的性质和应用。虽然它们之间存在区别,但它们之间也存在着联系和交叉。了解这三个概念及其之间的联系有助于更好地理解和应用它们在各个领域中的应用。
———END———
限 时 特 惠: 本站每日持续更新海量各大内部创业教程,永久会员只需109元,全站资源免费下载 点击查看详情
站 长 微 信: nanadh666



