过拟合:数据过度学习数据集,不能进行很好的泛化(不能很好的使用在其他的数据上);过拟合可以有两种情况:
1.样本分布有偏,或样本太少。
假设有1000套房子,按房子所处位置可以分为奢华地段,普通地段,贫困地段;
那不同地段可以有不同的房价水平,按照上文,房价=系数*面积
那不同的地段系数会有略微不同,但是整体还在一个水平,当我们构建的数据样本分布有偏,偏向于奢华地段的房子(比如800套奢华,100套普通,100套贫困)那模型结果就偏向奢华,但是实际情况房子分布水平可能是3:3:4的情况,那这个模型就过拟合了奢华地段的房子,所以模型整体效果会因为过拟合而偏低。
此时,扩大样本容量,是为了更多的接近总体分布。
2.模型太复杂。
由于样本模型太复杂,对于样本的拟合能力太强,我们希望模型学习通用的统计结果,但是复杂模型更容易把特殊的情况也学习了,比如,在某一个地区的贫民地段因为拆迁,房价很高,这是一个异常值,而模型却把这个地区的情况学习了,导致贫民地段房价预测偏高,拟合结果出现较大差异。
此时,通过正则化,是为了降低模型复杂性。
所以,解决过拟合,两个方向,一个是加样本,另一个是减少模型复杂性,另外还有其他一些方法(交叉验证等)。一般情况下,加样本是很难的,现实情况下,数据往往不够用。所以这个时候我们更需要正则化。
注:做模型时,要注意样本和总体关系,考虑样本是否能代表总体(分类变量看用卡方分布检验,连续变量用t检验)
岭回归&Lasso回归和正则有什么关系?
常用的正则表达式有L1,L2:
L1正则表达式:
L1正则表达式
L2正则表达式:
L2正则表达式
Lk正则表达式:
Lk正则表达式
机器学习把L1和L2叫正则化,统计学领域叫惩罚项,数学领域叫范数。
实际上,岭回归和Lasso回归就是在线性回归模型的基础上加上不同的正则因子,以降低模型复杂度来优化模型。
Lasso回归使用的是L1,岭回归使用的是L2
Lasso回归
Lasso回归是在线性回归的公式上直接加上L1正则惩罚性:
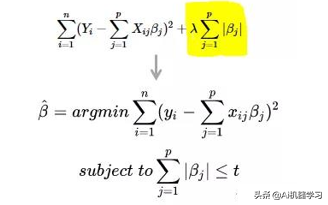
Lasso回归
岭回归
岭回归是在线性回归的公式上直接加上L2正则惩罚性:
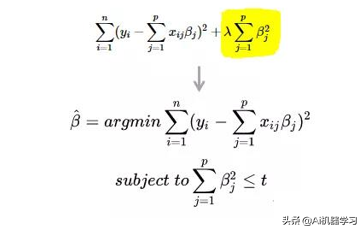
岭回归
正则化项怎么进行调节?
从Lasso回归和岭回归我们可以看到,实际上就是线性回归加一个惩罚因子,所以最终的模型不仅仅要考虑 – 最小,还要考虑惩罚项。
正则项其实就是线性变量的系数组合
如果,系数过大,那么变量的小变动,会导致,整个预测结果有较大变化
假如,y=bx,b=10000,当x从1001变为1003,y增加了20000
如果,系数过小,那么变量的小变动,会导致,整个预测结果没有什么变化
假如,y=bx,b=1,当x从1001变为1003,y增加了2
我们希望系数不宜过大,也不宜太小,我们可以通过λ进行调节惩罚项大小,同时也注意避免λ过大造成的欠拟合
岭回归&Lasso回归的区别
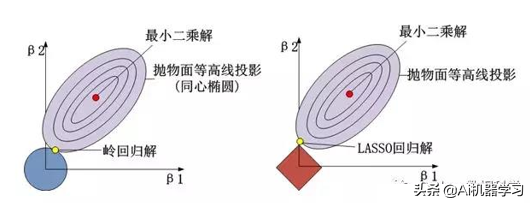
Lasso&岭回归
此处了解一下,不必深究有偏和无偏的概念
1. 线性回归求解为无偏估计,解为最小二乘解(红点)
2.岭回归&Lasso回归为有偏估计,解为圆和正则项交点(黄点)
从图形上看,岭回归解沿着正则项,正则项也为圆形,随着正则惩罚因子的变大,系数只会无限接近0而不会等于0,Lasso则可以沿着菱形到达0,所以L1也可以用来做变量选择,用来将弱变量剔除。
L1对于异常数据的容忍度高于L2,L1是照顾大部分的样本,L2是照顾所有的样本
怎么理解这句话呢?当有异常时,L2的波动变化较大,会放大异常值的大小,会使得模型更加不稳定。
当有异常值的时候,我们希望加大惩罚来抵消干扰。
当有异常时,- 的值会变大,此时需要加入更多的正则惩罚,而L2是系数的平方,加入的误差项是指数型增长的,此时可能放入更多也可能更少误差。(相对于L1)
随着我们对λ的调整,加入的正则项不稳定。当加入的误差越大,则会模型会做出更大的调整以应对该异常,从而牺牲到其他正常样本,而L1是线性增长,相对来说会更稳定,所以从下图上看,红线L1总体稳定性会相对于蓝色L2更加稳定。
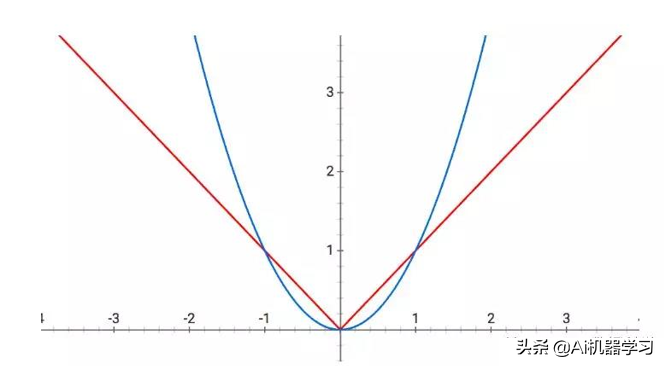
蓝色:岭回归,红色:Lasso回归 y:误差,x:正则大小
岭回归&Lasso回归对于多重共线性的影响?
上文提及,岭回归和Lasso回归能够降低多重共线性的影响。共线性得影响是不能消除,只能降低。
当对各个变量加入正则惩罚项时,会渐弱变量间的关系。
另一方面,通过增加样本间,变量间的差异,使得求解时多重共线性的非满秩矩阵变为满秩矩阵,从而可以更好的求解。
系数解:
θ = (XTX+λI)−1XTY
变为 :
θ = (XTX+Lk I)−1XTY
Lk为正则因子,I为单位矩阵
下章再介绍如何使用的使用Lasso回归和岭回归
本次分享到此为止,后续将继续分享,如对您有帮助,请关注并转发支持谢谢。
———END———
限 时 特 惠: 本站每日持续更新海量各大内部创业教程,永久会员只需109元,全站资源免费下载 点击查看详情
站 长 微 信: nanadh666



