很多著名的数学问题,长期得不到解决,最后被某位大神解决了,他给出的答案或许并没有人们想象的那么复杂。人们之所以长期找不到答案,并不是因为这个问题难度是空前的,只是思维太过平凡,没有去除那些干扰的因素从而看到问题的本质。

欧拉虽然出生在瑞士巴塞尔,也是在巴塞尔城完成了学业。但是后来他学成之后就再也没有回到瑞士了,俄国和德国是他职业生涯最重要的两站,欧拉的成果都写进了这两个国家的科学史里。虽然如此,欧拉毕生都没有更改过国籍,始终是瑞士籍。

哥尼斯堡大教堂
1727年,欧拉应圣彼得堡科学院的邀请到俄国,并在这里工作了14年,留下了大量的研究成果。1735年,在俄国收到一封德国大学生写的信,是想求教一道难题,这个问题在数学史上有个专有的名字——“哥尼斯堡七桥问题”。
这个问题是这样子的:在哥尼斯堡城的一个公园里,有七座桥将普雷格尔河中两个岛及岛与河岸连接起来。问是否可能从这四块陆地中任一块出发,恰好通过每座桥一次,再回到起点?
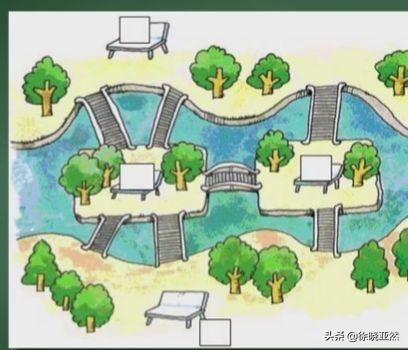
七桥位置分布
我们来简单分析一下这个问题,有7座桥,在每座桥只经过一次的情况下走完所有的陆地。猛一看,这个有点像是排列组合的问题,于是乎,我们可以遍历所有情况,然后分析这些路径不就解决问题了。说的有道理,于是就有7!种可能,也就是5040种,如果你真的遍历了这5040种路径,恭喜你,你得到了正确的答案。答案是不存在这样一种走法。
这个问题是困扰着哥尼斯堡的很多人,我相信肯定有人已经做过这样的暴力计算。人们一直对这个问题纠缠不清,应该是想从另外一方面得到解答,在那个根本不知道计算机是啥玩意的年代,没人愿意接受这样的粗暴解答。人们应该是在寻找一个判别依据,可以简单地对所有类似的问题进行分析,不限于桥的数量。还好哥尼斯堡这个公园里只有7座桥,还能接受,要是17座桥呢?没有计算机的年代,那还不得把人算死。
欧拉被这个问题吸引住了,1736年,时年29岁。欧拉特地到德国拜访了这个七桥现场。回到俄国之后,欧拉对这个问题进行了深入的研究,并在当年给出了七桥问题圆满的解答。

欧拉大神
下面,我们来欣赏一下欧拉的证明思路。
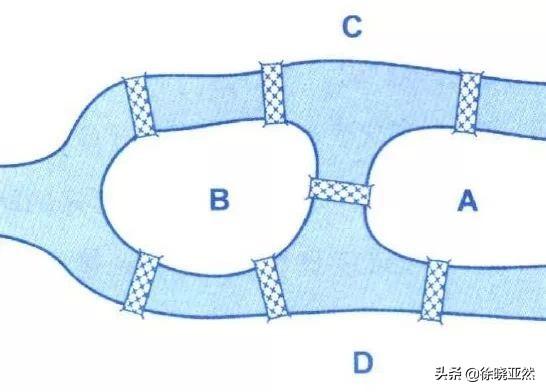
七桥问题简化 1
欧拉将这个问题抽象化,认为“每座桥只能走一次”对应着线段只能一笔画出,不可在原有基础再次描述;认为“四块分隔开的陆地”对应着就是平面上的四个分开的点;认为“七座桥”也就对应着平面上的七个分隔的线段。
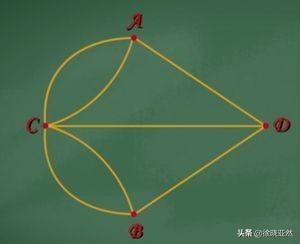
七桥问题简化 2
经过这么一类比,欧拉就将这个看似很多种考虑因素的问题一下子简化成一个“图形一笔画”的问题,事实上,两个问题完全等价。可以说,欧拉这么一处理,原先那些几千种的可能路径计算变得毫无意义,问题如此显而易见了。欧拉慧眼如炬,一下洞穿本质!
于是“七桥问题”就变成了下面这个图形能否一笔画的可能性了。这样的简化过后,欧拉得解决了“七桥问题”。说到证明,大家可能都会有点恐惧,脑海里都是在徘徊着公式,逻辑推理,动不动几十上百页,看着就让人心烦意乱。其实数学上还有些很精彩但是却趣味横生的证明,比如欧拉对于“七桥问题不可能性的证明”。
我们假设存在一种走法满足要求,于是我们从A点出发,遍历了所有桥,最终回到B点的路径,这里的A点叫起点,B叫终点,A,B两点不同。我们把走法中间经过的节点都叫做中间节点。因为这里是一笔画出来,所以每个中间点都必须有进有出,于是,只有当所有的中间节点都是偶数才会有解。如果进入这个点的次数和离开这个点的次数不同,那么就说明总有一条路径进入这个点就没有离开过,或者总有一条路径没有进入这个点就离开了,前者其实就是终点,后者就是起点,这是不符合行走规则的。所以,任何一个中间节点的路径必定是偶数个,不会是奇数个。于是我们得出来起点终点不同的一笔画条件:
中间节点经过的路径数必须是偶数个,起点和终点必须是奇数个。
那假如起点就是终点呢?就相当于我们环绕着七桥逛了一圈之后,又回到了起点。这里的分析跟上面类似,中间点路径仍然要是偶数个,但是由于这里的起点与终点重合,所以,经过起点的路径离开起点之后,最后又要再回到起点,于是,起点(终点)的路径的个数也必须是偶数个了。
于是,综上两种情况,可以一笔画的图形就必须满足:
图形里经过奇数条路径的点要么是2个(起点终点不同),要么就是0个(起点终点相同),除此之外别的所有的点的路径数都是偶数。
当然了这个图形必须是封闭的,否则就会有去无回!
很明显,“七桥问题中”4个点都是奇数个路径,不符合一笔画的条件,所以无解。想起小学时候,有个同学问我,能不能一笔写出一个“田”字,那个时候试了很久都没有答案,经过欧拉的分析,答案自是一目了然。
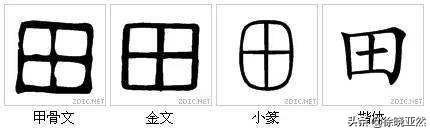
田 的一笔写法
这个证明简单吧,我想任何人只要对照着那张简化图形都可以明白欧拉的思路了,也没有人去怀疑这个证明的逻辑性,因为这样的推理逻辑实在自然,没有一点点绕弯的地方,甚至是没有任何技巧可言。就好比你问别人昨晚吃的什么,他平淡无奇地跟你说了一般的感觉!
原来有些著名问题的证明也如此接地气啊。有些人看明白了这个证明,心想,欧拉也不过如此啊,这个证明我也可以提出来啊,反正又没有什么高深的数学理论。事实上欧拉在这个问题的天才之处不在于后面关于几个规则的类比,而是前面将“七桥问题”改造成一个我们可以很容易分析的一笔画问题。从而避开了那些可能要算几千种的土办法。能够洞察天机,往往就已经将这个问题解决了大半,后面的解答过程就是水到渠成的事情了。

圣彼得堡大学
1736年,欧拉向圣彼得堡科学院递交了《哥尼斯堡的七座桥》的论文,给世人做了一个完美的解答。同时这篇论文也宣告了两门数学分支学科的诞生,拓扑学和图论。前面欧拉将问题抽象成一笔画图形的思想正是拓扑学里的等价变换,虽然外形改变了,但是我们需要的那个性质还是存在的。大家非常熟悉的“庞加莱猜想”正是拓扑学的根本性问题。关于图论,我又想起一个著名的问题,很多学编程的同学在学习递归算法的时候相信都曾被这个经典的问题虐过吧,我也是。这就是“八皇后问题”。

八皇后问题的一个解
说的是在国际象棋8×8的棋盘上放置8个皇后,使得所有的皇后不在同列,不在同行,也不在对角线上,问这样的摆法总共有多少种?高斯认为有76种解法,后来有人在棋类杂志上陆陆续续发表了40种解法,直到后来有人用图论的理论求解出八皇后问题一共有92个解。中学时代学习这个算法时,我就好奇图论到底是个什么玩意的学科,怎么就可以一下子确定出几十年都没有定论的八皇后问题呢?现在总算是有一点点了解了。
历史上的哥尼斯堡城曾经几易其主,到现在也并非是个安宁之地。但是这个小地方却因为这个问题流传在数学史上,很多人是因为一个故事而记住一座城市,而哥尼斯堡却是一个问题和一位伟大的数学巨人闻名于世。
———END———
限 时 特 惠: 本站每日持续更新海量各大内部创业教程,永久会员只需109元,全站资源免费下载 点击查看详情
站 长 微 信: nanadh666



