作为一名前端开发工程师,你可能有时会问:学习数据结构或者算法对于前端工程师有用么?
总的来说,这些基础学科在短期内收效确实甚微,但是我们首先不要将自己局限在前端工程师这点上,当我们把视野放到编程这个角度去说,数据结构算法一定是有用的,并且也是你未来的一个天花板。可以不花费集中的时间去学习这些内容,但是一定需要时常去学习一点,因为这些技能可以实实在在提升你写代码的能力。
这一篇文章的内容信息量会很大,代码也比较多,为了方便大家阅读,有些代码我会转成图片。
时间复杂度
在进入正题之前,我们先来了解下什么是时间复杂度。
通常使用最差的时间复杂度来衡量一个算法的好坏。
常数时间 O(1) 代表这个操作和数据量没关系,是一个固定时间的操作,比如说四则运算。
对于一个算法来说,可能会计算出操作次数为 aN + 1,N 代表数据量。那么该算法的时间复杂度就是 O(N)。因为我们在计算时间复杂度的时候,数据量通常是非常大的,这时候低阶项和常数项可以忽略不计。
当然可能会出现两个算法都是 O(N) 的时间复杂度,那么对比两个算法的好坏就要通过对比低阶项和常数项了。
概念
栈是一个线性结构,在计算机中是一个相当常见的数据结构。
栈的特点是只能在某一端添加或删除数据,遵循先进后出的原则

实现
每种数据结构都可以用很多种方式来实现,其实可以把栈看成是数组的一个子集,所以这里使用数组来实现
class Stack {
constructor() {
this.stack = []
}
push(item) {
this.stack.push(item)
}
pop() {
this.stack.pop()
}
peek() {
return this.stack[this.getCount() - 1]
}
getCount() {
return this.stack.length
}
isEmpty() {
return this.getCount() === 0
}
}
应用
题意是匹配括号,可以通过栈的特性来完成这道题目
var isValid = function (s) {
let map = {
'(': -1,
')': 1,
'[': -2,
']': 2,
'{': -3,
'}': 3
}
let stack = []
for (let i = 0; i < s.length; i++) {
if (map[s[i]] 0) return false
return true
};
其实在 Vue 中关于模板解析的代码,就有应用到匹配尖括号的内容。
队列
概念
队列是一个线性结构,特点是在某一端添加数据,在另一端删除数据,遵循先进先出的原则。

实现
这里会讲解两种实现队列的方式,分别是单链队列和循环队列。
单链队列
class Queue {
constructor() {
this.queue = []
}
enQueue(item) {
this.queue.push(item)
}
deQueue() {
return this.queue.shift()
}
getHeader() {
return this.queue[0]
}
getLength() {
return this.queue.length
}
isEmpty() {
return this.getLength() === 0
}
}
因为单链队列在出队操作的时候需要 O(n) 的时间复杂度,所以引入了循环队列。循环队列的出队操作平均是 O(1) 的时间复杂度。
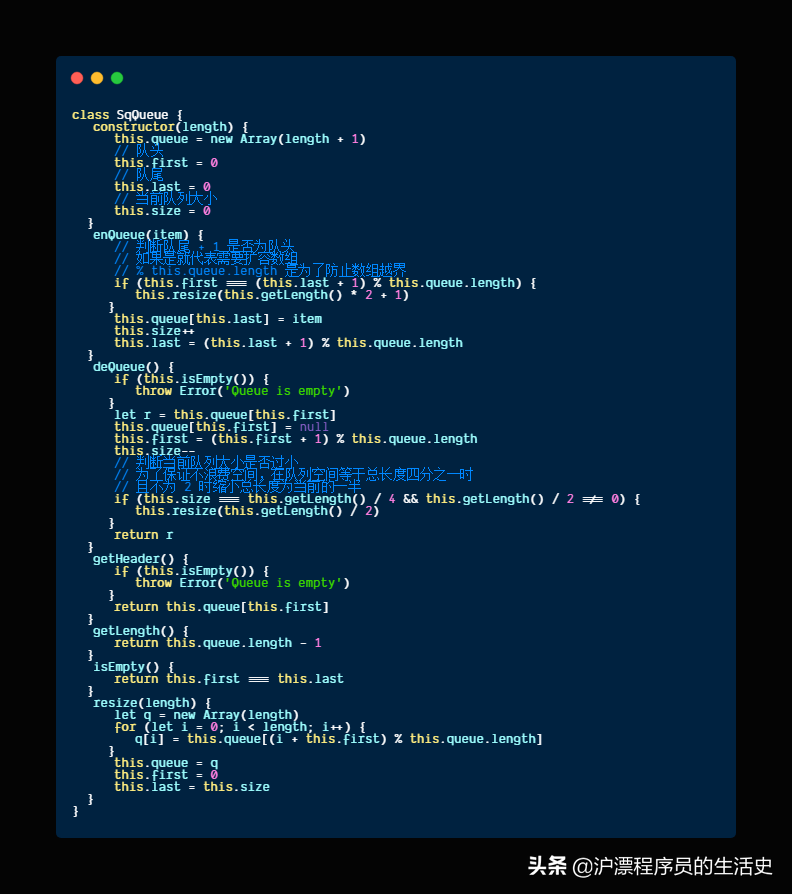
循环队列
我们直接看代码:
链表
概念
链表是一个线性结构,同时也是一个天然的递归结构。链表结构可以充分利用计算机内存空间,实现灵活的内存动态管理。但是链表失去了数组随机读取的优点,同时链表由于增加了结点的指针域,空间开销比较大。

实现
下面我们主要以单向链表为例。
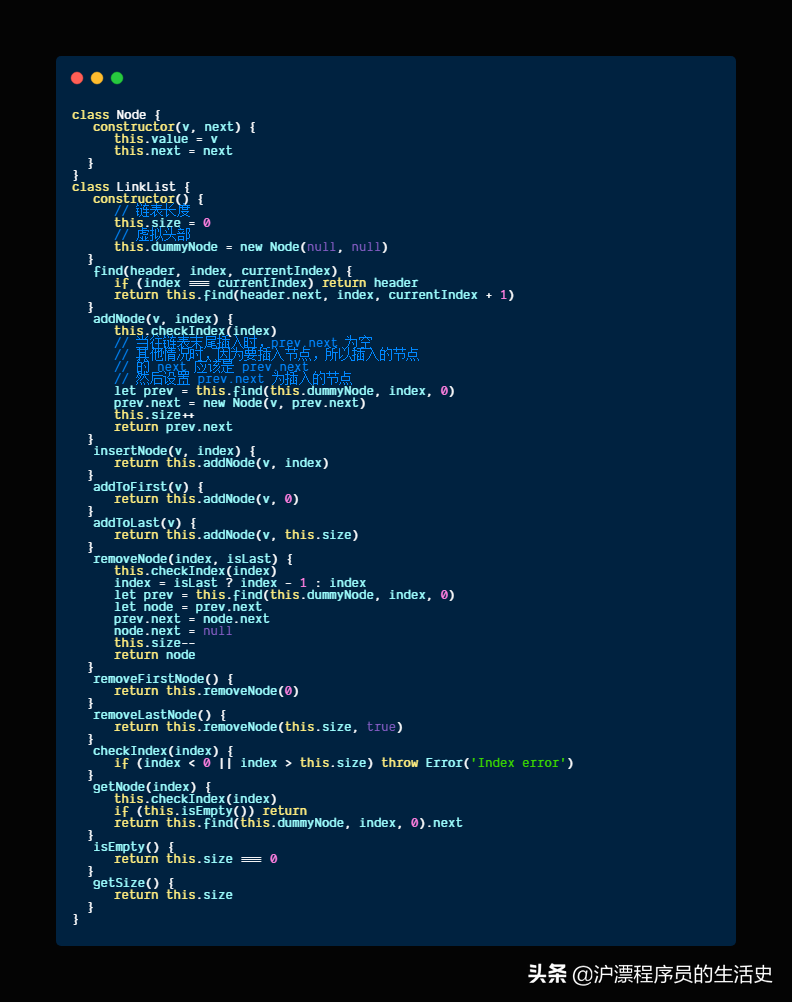
单向链表
树
二叉树
树拥有很多种结构,二叉树是树中最常用的结构,同时也是一个天然的递归结构。
二叉树拥有一个根节点,每个节点至多拥有两个子节点,分别为:左节点和右节点。树的最底部节点称之为叶节点,当一颗树的叶数量数量为满时,该树可以称之为满二叉树。

二分搜索树
二分搜索树也是二叉树,拥有二叉树的特性。但是区别在于二分搜索树每个节点的值都比他的左子树的值大,比右子树的值小。
这种存储方式很适合于数据搜索。如下图所示,当需要查找 6 的时候,因为需要查找的值比根节点的值大,所以只需要在根节点的右子树上寻找,大大提高了搜索效率。

实现
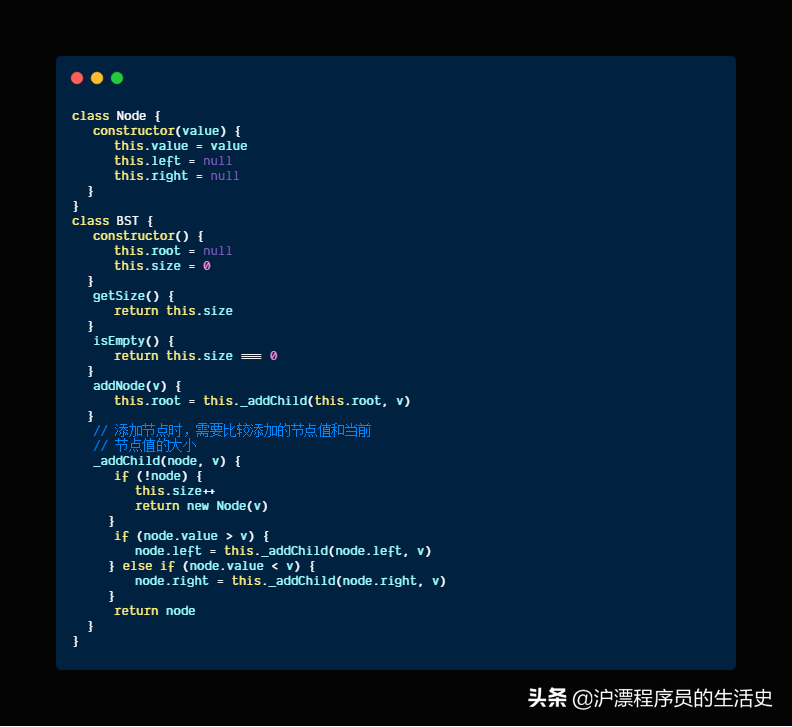
以上是最基本的二分搜索树实现,接下来实现树的遍历。
对于树的遍历来说,有三种遍历方法,分别是先序遍历、中序遍历、后序遍历。三种遍历的区别在于何时访问节点。在遍历树的过程中,每个节点都会遍历三次,分别是遍历到自己,遍历左子树和遍历右子树。如果需要实现先序遍历,那么只需要第一次遍历到节点时进行操作即可。
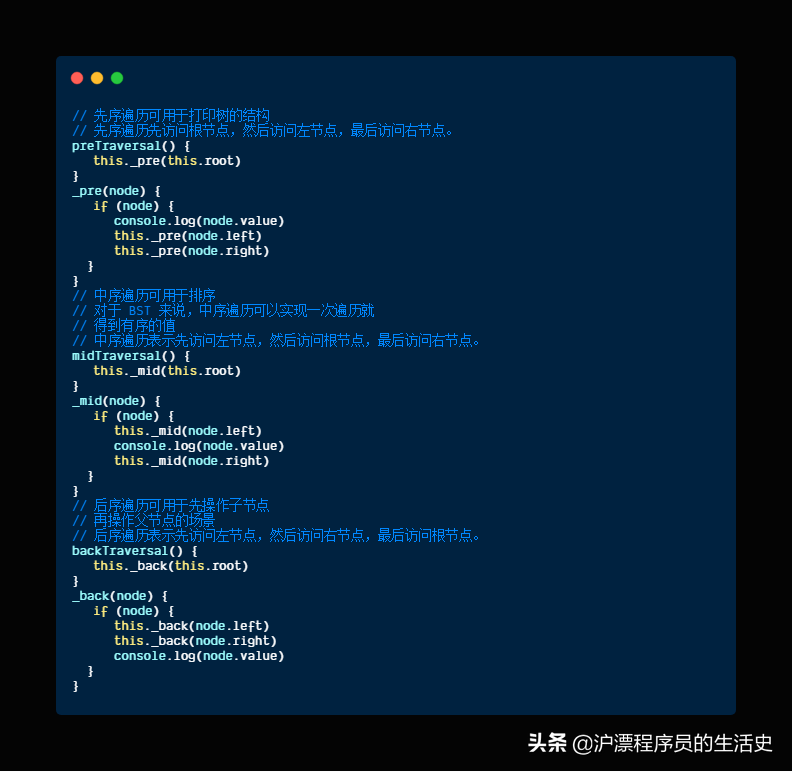
以上的这几种遍历都可以称之为深度遍历,对应的还有种遍历叫做广度遍历,也就是一层层地遍历树。对于广度遍历来说,我们需要利用之前讲过的队列结构来完成。

接下来先介绍如何在树中寻找最小值或最大数。因为二分搜索树的特性,所以最小值一定在根节点的最左边,最大值相反

向上取整和向下取整,这两个操作是相反的,所以代码也是类似的,这里只介绍如何向下取整。既然是向下取整,那么根据二分搜索树的特性,值一定在根节点的左侧。只需要一直遍历左子树直到当前节点的值不再大于等于需要的值,然后判断节点是否还拥有右子树。如果有的话,继续上面的递归判断。

排名,这是用于获取给定值的排名或者排名第几的节点的值,这两个操作也是相反的,所以这个只介绍如何获取排名第几的节点的值。对于这个操作而言,我们需要略微的改造点代码,让每个节点拥有一个 size 属性。该属性表示该节点下有多少子节点(包含自身)。

接下来讲解的是二分搜索树中最难实现的部分:删除节点。因为对于删除节点来说,会存在以下几种情况
对于前两种情况很好解决,但是第三种情况就有难度了,所以先来实现相对简单的操作:删除最小节点,对于删除最小节点来说,是不存在第三种情况的,删除最大节点操作是和删除最小节点相反的,所以这里也就不再赘述。

最后讲解的就是如何删除任意节点了。对于这个操作,T. 在 1962 年提出了解决这个难题的办法,也就是如何解决第三种情况。
当遇到这种情况时,需要取出当前节点的后继节点(也就是当前节点右子树的最小节点)来替换需要删除的节点。然后将需要删除节点的左子树赋值给后继结点,右子树删除后继结点后赋值给他。
你如果对于这个解决办法有疑问的话,可以这样考虑。因为二分搜索树的特性,父节点一定比所有左子节点大,比所有右子节点小。那么当需要删除父节点时,势必需要拿出一个比父节点大的节点来替换父节点。这个节点肯定不存在于左子树,必然存在于右子树。然后又需要保持父节点都是比右子节点小的,那么就可以取出右子树中最小的那个节点来替换父节点。

AVL 树
概念
二分搜索树实际在业务中是受到限制的,因为并不是严格的 O(logN),在极端情况下会退化成链表,比如加入一组升序的数字就会造成这种情况。
AVL 树改进了二分搜索树,在 AVL 树中任意节点的左右子树的高度差都不大于 1,这样保证了时间复杂度是严格的 O(logN)。基于此,对 AVL 树增加或删除节点时可能需要旋转树来达到高度的平衡。
实现
因为 AVL 树是改进了二分搜索树,所以部分代码是于二分搜索树重复的,对于重复内容不作再次解析。
对于 AVL 树来说,添加节点会有四种情况

对于左左情况来说,新增加的节点位于节点 2 的左侧,这时树已经不平衡,需要旋转。因为搜索树的特性,节点比左节点大,比右节点小,所以旋转以后也要实现这个特性。
旋转之前:new < 2 < C < 3 < B < 5 < A,右旋之后节点 3 为根节点,这时候需要将节点 3 的右节点加到节点 5 的左边,最后还需要更新节点的高度。
对于右右情况来说,相反于左左情况,所以不再赘述。
对于左右情况来说,新增加的节点位于节点 4 的右侧。对于这种情况,需要通过两次旋转来达到目的。
首先对节点的左节点左旋,这时树满足左左的情况,再对节点进行一次右旋就可以达到目的。

Trie
概念
在计算机科学,trie,又称前缀树或字典树,是一种有序树,用于保存关联数组,其中的键通常是字符串。
简单点来说,这个结构的作用大多是为了方便搜索字符串,该树有以下几个特点

实现
总得来说 Trie 的实现相比别的树结构来说简单的很多,实现就以搜索英文字符为例。

并查集
概念
并查集是一种特殊的树结构,用于处理一些不交集的合并及查询问题。该结构中每个节点都有一个父节点,如果只有当前一个节点,那么该节点的父节点指向自己。
这个结构中有两个重要的操作,分别是:

实现

堆
概念
堆通常是一个可以被看做一棵树的数组对象。
堆的实现通过构造二叉堆,实为二叉树的一种。这种数据结构具有以下性质。
将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
优先队列也完全可以用堆来实现,操作是一模一样的。
实现大根堆
堆的每个节点的左边子节点索引是 i * 2 + 1,右边是 i * 2 + 2,父节点是 (i – 1) /2。
堆有两个核心的操作,分别是 和 。前者用于添加元素,后者用于删除根节点。
的核心思路是一路将节点与父节点对比大小,如果比父节点大,就和父节点交换位置。
的核心思路是先将根节点和末尾交换位置,然后移除末尾元素。接下来循环判断父节点和两个子节点的大小,如果子节点大,就把最大的子节点和父节点交换。

下面是代码实现方案

小结
这一篇主要介绍了一些比较常见的数据结构,当然还有其他更难的数据结构,这次没有放进来,是因为小编觉得如果能够掌握这些常见的内容已经足够解决大部分的问题了。当然你如果还想继续深入学习数据结构,可以阅读《算法第四版》以及在 中去实践。
———END———
限 时 特 惠: 本站每日持续更新海量各大内部创业教程,永久会员只需109元,全站资源免费下载 点击查看详情
站 长 微 信: nanadh666



